บทความตอนนี้จะบอกว่าเป็นตอนต่อจากครั้งที่แล้วก็ได้ครับ เพราะอยากจะพูดถึงการเขียนขั้นตอนการคำนวณที่น่าจะมีความถูกต้องกว่ามาก ให้ได้ดูกัน เหตุที่อาจจะนำเสนอเรื่องนี้ก็เพราะว่าได้เห็นวิธีการทำงานของเด็กนักเรียนหลายๆคน จากต่างสถานทีกันแต่มีการแสดงขั้นตอนการทำงานที่แปลกๆ คล้ายๆกัน ในลักษณะที่ผิดวิธีการหรือเขียนขั้นตอนแบบตามใจฉันแต่ได้คำตอบถูก โดยอยากให้สังเกตจากตัวอย่างต่อไปนี้ครับ
จะเห็นว่า คำตอบที่ได้เดิมกันแต่ความถูกต้องของขั้นตอนต่างกันอย่างๆ
คำถาม แล้วปัญหาอยู่ที่ไหน ???
คำตอบ ถ้ามองดูแบบผิวเผิน ก็ไม่น่าจะมีปัญหาอะไรในเมื่อคำตอบไม่ต่างกัน แต่ในความเป็นจริงแล้วผิดอย่างมาก เพราะวิชาคณิตศาสตร์เป็นวิชาพื้นฐานที่เน้นการฝึกฝนให้ผู้เรียนคิดและทำงานอย่างมีเหตุผล เป็นขั้นเป็นตอน ตามหลักเกณฑ์ต่างๆที่มีอยู่ กล่าวคือ ในการแสดงขั้นตอนที่ลักษณะของโจทย์เป็นการเขียนเครื่องหมายเท่ากับ (=) ต่อเนื่องกันไปเรื่อยๆ จนได้คำตอบที่ต้องการ เราต้องคำนึงถึง ความเท่ากันของตัวเลขทั้ง 2 ข้างของสมการ โดยอาศัยหลักการ ที่เราเรียกว่า กฎการถ่ายทอด (สมบัติการถ่ายทอด ก็แล้วแต่จะเรียกกันไป) ที่ว่า a = b และ b = c แล้ว a = c เป็นเหตุผลเบื้องหลังของการเขียนขั้นตอนการทำงานแต่ไม่มีใครชี้ให้เด็กเห็นเท่าที่ควร
และที่ผมรู้สึกเป็นห่วงมากที่สุดคือ... การเขียนที่ขั้นตอนที่ดูแปลกของเด็ก ผมคิดว่าน่าจะสะท้อนถึงระบบกระบวนการคิดที่ไม่ดี ถ้าเด็กทำจนติดเป็นนิสัยก็จะทำให้เด็กคิดและทำแบบสับสนไม่เป็นขั้นตอน ส่งผลกับการเรียนและการทำงานต่อไปในอนาคต
โดยส่วนตัวแล้ว ผมไม่เคยดีใจเลยที่่เด็กตอบคำถามถูกต้อง แต่ไม่สามารถแสดงเหตุผลโดยอ้างอิงถึงหลักการที่ถูกต้องได้ หรือ อธิบายสิ่งที่ทำได้อย่างชัดเจน
และถ้าเด็กที่เป็นอนาคตของชาติของเราเป็นแบบนี้กันมากๆ ต่อไปเราจะไปต่อกันได้อย่างไร...
วันพฤหัสบดีที่ 25 เมษายน พ.ศ. 2556
วันพฤหัสบดีที่ 18 เมษายน พ.ศ. 2556
การทำโจทย์คณิตศาสตร์ให้เหมาะสม
เมื่อเร็วๆนี้ มีนักเรียนคนหนึ่งของผมมาท้วงติงผมว่า คุณครูที่โรงเรียนบอกว่า หนูทำงานที่เป็นการแก้สมการผิดวิธี ครูที่สอนหนูมา(หมายถึงครูสอนพิเศษ) สอนไม่ต้องถูกต้อง ทำให้เด็กเกิดความสับสน ผมเลยต้องทำความเข้าใจกับลูกศิษย์คนนี้อยู่พักใหญ่ ทำให้ผมเกิดความคิดที่จะเขียนบทความตอนนี้ขึ้น ซึ่งผมคิดว่าเป็นเรื่องที่สำคัญมากที่สุดเรื่องหนึ่งในการเรียนวิชาคณิตศาสตร์ คือ เรื่องของวิธีการทำงานให้เหมาะสมกับกาละเทศะ แต่ก่อนอื่นขอให้พิจารณาวิธีการแก้สมการ ทั้ง 2 วิธี ด้านล่างนี้ ก่อน
วิธีแรกเป็นวิธีมาตราฐาน เป็นการแสดงขั้นตอนที่ถูกต้อง(ที่สุด)ในการแก้สมการ เป็นวิธีการที่ครูในโรงเรียนควรสอนในห้อง ให้เด็กนักเรียนเกิดความเข้าใจในแนวคิดในเรื่องการใช้หลักของการเท่ากันของสมการมาแก้ไขปัญญา และเป็นสิ่งที่เด็กทุกๆต้องเรียนรู้และทำจะเกิดเป็นทักษะและความเข้าใจให้ดีก่อนเป็นพื้นฐาน ก่อนที่จะทำไปใช้วิธีลัดอื่นๆ
วิธีที่ 2 เป็นวิธีลัด ต้องบอกว่าเป็นการแสดงวิธีทำที่ไม่ดีนัก แต่เป็นที่นิยมในปัจจุบันเพราะทำให้การเขียนสั้นลงประหยัดเวลาในการทำงาน เหมาะสมหรับใช้ในการทำข้อสอบที่ไม่เน้นการแสดงขั้นตอนที่ถูกต้อง
ไม่เหมาะกับการทำการบ้านส่งครู
อย่างไรก็ดี ในการทำงานจริงเราต้องเลือกวิธีการทำงานให้ถูกต้องเหมาะสม และในการทำงานต่างๆที่สำคัญ ต้องไม่หลงลืมคิดถึงแนวคิดและพื้นฐานที่ถูกต้องด้วย อย่างน้อยถ้าคิดจะทำด้วยวิธีลัดต่างๆ ก็ต้องสามารถจะอธิบายถึงที่มาที่ไปและให้เหตุผลมาหลักการพื้นฐานที่ถูกต้องได้ด้วย จึงจะเป็นการดี
ในประเด็นนี้ผมต้องฝากให้ทุกคนที่มีส่วนเกี่ยวข้อง ช่วยกันบอกและย้ำเตือนเด็กนักเรียนของเราด้วย เพราะถ้าเด็กของเรายึดแต่จะทำวิธีลัดหรือใช้สูตรลัดเพียงอย่างเดียว จะเป็นอันตรายกับรากฐานในระบบการเรียนการสอนวิชาคณิตศาสตร์ของเรา และทำเป็นการทำลายระบบความคิดในสมองของเด็กด้วย
วิธีแรกเป็นวิธีมาตราฐาน เป็นการแสดงขั้นตอนที่ถูกต้อง(ที่สุด)ในการแก้สมการ เป็นวิธีการที่ครูในโรงเรียนควรสอนในห้อง ให้เด็กนักเรียนเกิดความเข้าใจในแนวคิดในเรื่องการใช้หลักของการเท่ากันของสมการมาแก้ไขปัญญา และเป็นสิ่งที่เด็กทุกๆต้องเรียนรู้และทำจะเกิดเป็นทักษะและความเข้าใจให้ดีก่อนเป็นพื้นฐาน ก่อนที่จะทำไปใช้วิธีลัดอื่นๆ
วิธีที่ 2 เป็นวิธีลัด ต้องบอกว่าเป็นการแสดงวิธีทำที่ไม่ดีนัก แต่เป็นที่นิยมในปัจจุบันเพราะทำให้การเขียนสั้นลงประหยัดเวลาในการทำงาน เหมาะสมหรับใช้ในการทำข้อสอบที่ไม่เน้นการแสดงขั้นตอนที่ถูกต้อง
ไม่เหมาะกับการทำการบ้านส่งครู
อย่างไรก็ดี ในการทำงานจริงเราต้องเลือกวิธีการทำงานให้ถูกต้องเหมาะสม และในการทำงานต่างๆที่สำคัญ ต้องไม่หลงลืมคิดถึงแนวคิดและพื้นฐานที่ถูกต้องด้วย อย่างน้อยถ้าคิดจะทำด้วยวิธีลัดต่างๆ ก็ต้องสามารถจะอธิบายถึงที่มาที่ไปและให้เหตุผลมาหลักการพื้นฐานที่ถูกต้องได้ด้วย จึงจะเป็นการดี
ในประเด็นนี้ผมต้องฝากให้ทุกคนที่มีส่วนเกี่ยวข้อง ช่วยกันบอกและย้ำเตือนเด็กนักเรียนของเราด้วย เพราะถ้าเด็กของเรายึดแต่จะทำวิธีลัดหรือใช้สูตรลัดเพียงอย่างเดียว จะเป็นอันตรายกับรากฐานในระบบการเรียนการสอนวิชาคณิตศาสตร์ของเรา และทำเป็นการทำลายระบบความคิดในสมองของเด็กด้วย
ตอบโจทย์ปลา 250-300กรัม
มีผู้ตั้งคำถามเกี่่ยวกับโจทย์บัญญัติไตรยางค์ที่น่าสนใจมาครับ โดยคำถามถามว่า
ปลา 250-300 กรัม คิดเป็น 1 แพ็ค แล้วถ้าปลา 21 แพ็ค คิดเป็นกี่กรัม(ค่ะ)
วิธีทำ
ปลา 1 แพ็ค มีน้ำหนักระหว่าง 250 - 300 กรัม
ปลา 21 แพ็ค มีน้ำหนักระหว่าง 250 x 21 ถึง 300 x 21 = 5250 ถึง 6200 กรัม
หรือจะเปลี่ยนหน่วยเป็นกิโลกรัม จะได้ 5.250 ถึง 6.200 กิโลกรัม
อย่าลืมนะครับว่า....การทำโจทย์ในเรื่องนี้ ต้องนำสิ่งที่โจทย์ถามมาอยู่ทางขวาเสมอ
ขอบคุณสำหรับคำถามดีๆครับ
ปลา 250-300 กรัม คิดเป็น 1 แพ็ค แล้วถ้าปลา 21 แพ็ค คิดเป็นกี่กรัม(ค่ะ)
วิธีทำ
ปลา 1 แพ็ค มีน้ำหนักระหว่าง 250 - 300 กรัม
ปลา 21 แพ็ค มีน้ำหนักระหว่าง 250 x 21 ถึง 300 x 21 = 5250 ถึง 6200 กรัม
หรือจะเปลี่ยนหน่วยเป็นกิโลกรัม จะได้ 5.250 ถึง 6.200 กิโลกรัม
อย่าลืมนะครับว่า....การทำโจทย์ในเรื่องนี้ ต้องนำสิ่งที่โจทย์ถามมาอยู่ทางขวาเสมอ
ขอบคุณสำหรับคำถามดีๆครับ
วันศุกร์ที่ 5 เมษายน พ.ศ. 2556
ทศวรรษ ศตวรรษและสหัสวรรษ
วันนี้ผมอยากจะเอาเรื่องของ ทศวรรษ ศตวรรษและสหัสวรรษ ที่เป็นภาษาอังกฤษ มาร่วมแบ่งปันกันครับ
ทศวรรษ แปลว่า 10 ปี มาจากคำว่า ทศ + วรรษ
ทศ แปลว่า 10 มักเคยเห็นคำว่า ทศ จากคำว่า ทศกัณฐ์ (10 คอหรือ10 เศียร) ที่เป็นยักษ์ในเรื่องรามเกียรติ์ และทศพิธราชธรรม เป็นคุณธรรม 10 ประการของพระราชาหรือผู้ปกครอง
วรรษ แปลว่า ปี, พรรษ, ฤดูฝน
ในภาษาอังกฤษ มีว่า 10 ปี นั้นตรงกับคำว่า decade นอกจากคำนี้แล้วยังมีวิธีการ บอกช่วงเวลา 10 ปี อีกแบบเช่น
1250s หมายถึง ช่วงเวลา 10 ปีที่นับจาก ค.ศ. 1250 - 1259
1980s หมายถึง ช่วงเวลา 10 ปีที่นับจาก ค.ศ. 1980 - 1989
2000s หมายถึง ช่วงเวลา 10 ปีที่นับจาก ค.ศ. 2000 - 2009
2030s หมายถึง ช่วงเวลา 10 ปีที่นับจาก ค.ศ. 2030 - 2039
หรือ บางครั้งก็ย่อรูป เป็น 40s ก็เคยเห็นครับ หมายถึงช่วง 10ปี ระหว่าง 40 - 49
ศตวรรษ แปลว่า 100 ปี มาจากคำว่า ทศ + วรรษ
ศต แปลว่า 100
ในภาษอังากฤษ มีว่า 100 ปี นั้นตรงกับคำว่า century นอกจากคำนี้แล้วยังมีวิธีการ นับ ช่วงเวลา 100 ปี ด้วย เช่น
the 1st century หมายถึง ศตวรรษที่ 1 นับจาก ค.ศ. 1 - 100
(เริ่ม 1 มกราคม ค.ศ. 1 ถึงวันที่ 31 ธันวาคม ค.ศ. 100)
the 2nd century หมายถึงศตวรรษที่ 2 นับจาก ค.ศ. 101 - 200
(เริ่ม 1 มกราคม ค.ศ. 101 ถึงวันที่ 31 ธันวาคม ค.ศ. 200)
the 3rd century หมายถึงศตวรรษที่ 3 นับจาก ค.ศ. 201 - 300
(เริ่ม 1 มกราคม ค.ศ. 201 ถึงวันที่ 31 ธันวาคม ค.ศ. 300)
the 4th century หมายถึงศตวรรษที่ 4 นับจาก ค.ศ. 301 - 400
(เริ่ม 1 มกราคม ค.ศ. 301 ถึงวันที่ 31 ธันวาคม ค.ศ. 400)
the 15th century หมายถึงศตวรรษที่ 15 นับจาก ค.ศ. 1401 - 1500
(เริ่ม 1 มกราคม ค.ศ. 1401 ถึงวันที่ 31 ธันวาคม ค.ศ. 1500)
the 19th century หมายถึงศตวรรษที่ 19 นับจาก ค.ศ. 1801 - 1900
(เริ่ม 1 มกราคม ค.ศ. 1801 ถึงวันที่ 31 ธันวาคม ค.ศ. 1900)
คำถาม แล้วปัจจุบัน เราอยู่ในช่วงต้นของศตวรรษ ที่เท่าไหร่
คำตอบ ปีนี้เป็นปี ค.ศ. 2013 ซึ่งอยู่ระหว่าง ปี ค.ศ. 2000 - 2100 ซึ่งตรงกับ ศตวรรษที่ 21 หรือเขียนเป็นแบบฝรั่งว่า the 21st century หมายถึง ศตวรรษที่ 21 นับจาก ค.ศ. 2001 - 2100 (เริ่ม 1 มกราคม ค.ศ. 2001 ถึงวันที่ 31 ธันวาคม ค.ศ. 2100)
สหัสวรรษ แปลว่า 1,000 ปี มาจากคำว่า สหัส + วรรษ
สหัส แปลว่า 1,000 เราเคยเห็นว่านี้ จากคำว่า สหัสเดชา (ผู้ที่มีฤิทธิ์ 1000 อย่าง) เป็นชื่อของยักษ์ในเรื่องรามเกียรติ์
ในภาษาอังกฤษ มีว่า 1000 ปี นั้นตรงกับคำว่า millennium
คำถาม แล้วตอนนี้เราอยู่ สหัสวรรษที่เท่าไหร่ กัน
คำตอบ ปัจจุบัน คือ ปีค.ศ. 2013 ซึ่งอยู่ระหว่าง ปี ค.ศ. 2001 - 3000 ตรงกับ สหัสวรรษที่ 3 ครับ
วันพฤหัสบดีที่ 4 เมษายน พ.ศ. 2556
อธิบายเพิ่มเติมโจทย์สมการเศษส่วน
มีน้องคนหนึ่งยังไม่เข้าใจ วิธีทำเกี่ยวกับโจทย์ การแก้สมการเศษส่วน ในหัวข้อ คณิตศาสตร์: การแก้สมการตอนที่8 ผมเลยอยากจะขออธิบายเพิ่มเติม โดยข้อความที่เขียนมามีว่า
คือว่าข้อ 2 อ่ะครับ 4x+12 = x-18 มันมาได้ไงอ่ะครับ 2x ส่วน 3 มาเอาไปคูณ ค.ร.น 6 แล้วมันได้ เท่ากับ 2 x คูณ 6 = 12x แล้ว 3 คูณ 6 แล้วจะได้ 18 มันต้องเท่ากับ 12x ส่วน 18 ไม่ใช่หรอครับ
ประเด็นที่ 1 ในการแก้สมการที่เป็นเศษคือ การนำค.ร.น. (ตัวคูณร่วมน้อยที่สุด) มาคูณทั้ง 2 ข้างของสมการ และถ้าตัวเลขมีหลายตัว การเขี่ยนที่ดี ต้องใช้วงเล็บคั้นไว้ป้องกันความผิดพลาด เพราะจะทำให้คูณเลขผิดได้ ตรงนี้ขอให้สังเกตและดูเปรียบเทียบจากตัวอย่างทั้ง 2 และจุดประสงค์หลักของการนำค.ร.น. มาคูณเพื่อการกำจัดตัวส่วนด้านล่างออกไปนั้นเอง
ประเด็นที่ 2 เมื่อเราต้องการคูณตัวเลขนอกวงเล็บกับเลขที่อยู่ในวงเล็บ เราจะใช้กฎการกระจายหรือการแจกแจงมาใช้ คือ ax(b + c) = axb + axc หรือ อาจจะจำง่ายๆว่า เลขที่อยู่นอกวงเล็บต้องคูณกับเลขทุกตัวที่อยู่ในวงเล็บ ก็ได้
ประเด็นที่ 3 เป็นสิ่งที่น้องสงสัย เป็นเรื่องการการคูณเศษส่วน เราจะใช้หลักการที่ว่า นำตัวเศษคูณกับตัวเศษ และ ตัวส่วนคูณกับตัวส่วน ถ้าเป็นจำนวนเต็มให้ถือว่าเป็นตัวเศษ เนื่องจากจำนวนเต็มทุกตัวมีส่วนเป็นเลข 1 เสมอ เช่น 6 = 6/1 , -3 = -3/1 เป็นต้น
แต่ในโจทย์ลักษณะนี้ เรานำคูณด้วย 6 เพื่อนำมาตัดทอนกัน ตัวส่วนที่อยู่ด้านทั้งสองคือ 3 กับ 6 ซึ่่ง 6/3 = 2 เมื่อนำไปคูณกับ 2x แล้วจึงได้ 4x ผลก็คือ เศษส่วนจะหายไป
อีกอย่างหนึ่งที่น้องเขียนมาว่า มันต้องเท่ากับ 12x ส่วน 18 คงจะมีความสับสนกับเรื่องของการ นำค.ร.น. มาคูณทั้งเศษและส่วน เพื่อทำให้ตัวส่วนด้านล่างเท่ากัน ตรงนี้เราใช้กรณีของการบวก - ลบเศษส่วนครับ
ขอให้สังเกต ตัวอย่างด้านล่างอีกครั้งนะครับ
ถึงตรงนี้หวังว่า น้องน่าพอจะเข้าใจมากขึ้นนะครับ แต่ถ้าต้องการให้ทำตัวอย่างเพิ่มเติมก็บอกมาได้ครับ
วันพุธที่ 3 เมษายน พ.ศ. 2556
โจทย์คณิตศาสตร์-ภาษาอังกฤษ
I want to know The minimum value of the function
ฉันอยากทราบคำต่ำสุดของฟังก์ชั่นต่อไปนี้
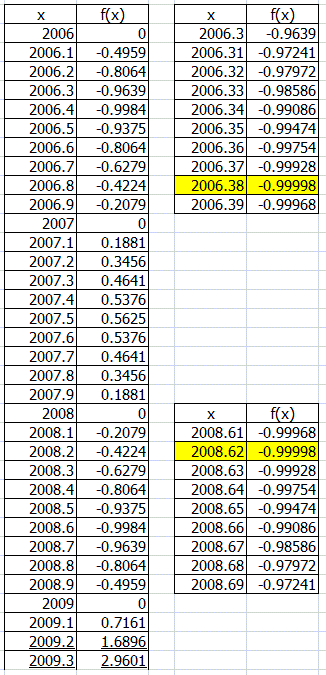
1. f(x)=(x-2006)(x-2007)(x-2008)(x-2009) and
2. f(x)=(2004cos2005x-2006)^2+2007
I have spent many days solving these question. But I cannot show you the answers by using algebraic method. And I do not sure that the answers would correct. I just use Excel to find them and choose the best one as the answer for each problem. I hope that you would be satisfied the answers and the way I show you. Thank you so much for your questions.
ผมได้ใช้เวลาหลายวันในการคิดแก้โจทย์ปัญหานี้ แต่ผมไม่สามารถแสดงคำตอบฝให้คุณดูได้ด้วยวิธีการทางพีชคณิต แล้วผมก็ได้แน่ใจในคำตอบว่าถูก ผมเพียงแต่ใช้โปรกแกรมช่วยผมหาคำตอบและเลือกคำตอบที่น่าจะดีที่สุด ผมหวังว่าคุณคงจะพอใจกับคำตอบและวิธีการแสดงคำตอบที่ทำให้คุณดู ขอบคุณมากๆสำหรับคำถาม
1. f(x)=(x-2006)(x-2007)(x-2008)(x-2009)
Answers the minimum value are x= 2006.38, f(x) = -0.9998 and x = 2008.62, f(x) = -0.9998
2. f(x)=(2004cos2005x-2006)^2+2007
Answers the minimum value is x = 9100, f(x) = 2007.031537
สมัครสมาชิก:
ความคิดเห็น (Atom)